Informar adecuadamente la actividad desarrollada en este trabajo práctico.
Implementar un filtro activo.
Medir sus parámetros.
2) Contenidos:
Principios de funcionamiento de un filtro pasivo y activo. Modelización. Análisis de models circuitales. Transferencia y respuesta en frecuencia.
Materiales necesarios:
2 circuitos integrados 741.
Resistores varios.
Capacitores varios.
Filtro Activo:
Un filtro activo es un filtro electrónico analógico distinguido por el uso de uno o más componentes activos (que proporcionan una cierta forma de amplificación de energía), que lo diferencian de los filtros pasivos que solamente usan componentes pasivos. Típicamente este elemento activo puede ser un tubo de vacío, un transistor o un amplificador operacional.
Un filtro activo puede presentar ganancia en toda o parte de la señal de salida respecto a la señal de entrada. En su implementación se combinan elementos activos y pasivos, siendo frecuente el uso de amplificadores operacionales, que permite obtener resonancia y un elevado factor Q sin el empleo de bobinas.
Se pueden implementar, entre otros, filtros paso bajo, paso alto, paso banda.

Un filtro pasa bajo corresponde a un filtro caracterizado por permitir el paso de las frecuencias más bajas y atenuar las frecuencias más altas. El filtro requiere de dos terminales de entrada y dos de salida, de una caja negra, también denominada cuadripolo o bipuerto, así todas las frecuencias se pueden presentar a la entrada, pero a la salida solo estarán presentes las que permita pasar el filtro. De la teoría se obtiene que los filtros están caracterizados por sus funciones de transferencia, así cualquier configuración de elementos activos o pasivos que consigan cierta función de transferencia serán considerados un filtro de cierto tipo.
En particular la función de transferencia de un filtro pasa bajo de primer orden corresponde a:

donde la constante K es sólo una ponderación correspondiente a la ganancia del filtro, y la real importancia reside en la forma de la función de transferencia,la cual determina el comportamiento del filtro. En la función de transferencia anterior OMEGAc corresponde a la frecuencia de corte propia del filtro, aquel valor de frecuencia para el cual la amplitud de la señal de entrada se atenua 3 dB.

Filtro pasa-bajo:
Un filtro paso alto (HPF) es un tipo de filtro electrónico en cuya respuesta en frecuencia se atenúan las componentes de baja frecuencia pero no las de alta frecuencia, éstas incluso pueden amplificarse en los filtros activos. La alta o baja frecuencia es un término relativo que dependerá del diseño y de la aplicación.

Filtro Pasa-banda:
Un filtro paso banda es un tipo de filtro electrónico que deja pasar un determinado rango de frecuencias de una señal y atenúa el paso del resto.
Un circuito simple de este tipo de filtros es un circuito RLC (resistencia, bobina y condensador) en el que se deja pasar la frecuencia de resonancia, que sería la frecuencia central (fc) y las componentes frecuenciales próximas a ésta, en el diagrama hasta f1 y f2. No obstante, bastaría con una simple red resonante LC.
Otra forma de construir un filtro paso banda puede ser usar un filtro paso bajo en serie con un filtro paso alto entre los que hay un rango de frecuencias que ambos dejan pasar. Para ello, es importante tener en cuenta que la frecuencia de corte del paso bajo sea mayor que la del paso alto, a fin de que la respuesta global sea paso banda (esto es, que haya solapamiento entre ambas respuestas en frecuencia).
Un filtro ideal sería el que tiene unas bandas pasante y de corte totalmente planas y unas zonas de transición entre ambas nulas, pero en la práctica esto nunca se consigue, siendo normalmente más parecido al ideal cuando mayor sea el orden del filtro, para medir cuanto de "bueno" es un filtro se puede emplear el denominado factor Q. En filtros de órdenes altos suele aparecer un rizado en las zonas de transición conocido como efecto Gibbs.
Un filtro paso banda más avanzado sería los de frecuencia móvil, en los que se pueden variar algunos parámetros frecuenciales, un ejemplo es el circuito anterior RLC en el que se sustituye el condensador por un diodo varicap o varactor, que actúa como condensador variable y, por lo tanto, puede variar su frecuencia central.
Realmente resulta realmente complicado construir un filtro paso banda ideal (y, en general, filtros de respuesta ideal) en el mundo analógico, esto es, a base de componentes pasivos como inductancias, condensadores o resistores, y activos como operacionales o simples transistores. Sin embargo, si nos trasladamos al procesado digital de señales, resulta sorprendente ver cómo podemos construir respuestas en frecuencia prácticamente ideales, ya que en procesado digital de señal manejamos realmente vectores con valores numéricos (que son señales discretas en el tiempo), en lugar de señales continuas en el tiempo. Todo ello, no obstante, tiene una limitación importante: cuanto mayor precisión se requiera, mayor frecuencia de muestreo necesitaremos, y ello directamente implica un consumo de RAM y CPU superiores. Por ello, al menos con la tecnología de la que hoy día disponemos, resultaría inviable implementar filtros digitales ideales para radiofrecuencia, aunque en procesado de audio digital sí es posible, dado que el rango de frecuencias que ocupa no supera los 20 kHz.
Aplicaciones
Estos filtros tienen aplicación en ecualizadores de audio, haciendo que unas frecuencias se amplifiquen más que otras.
Otra aplicación es la de eliminar ruidos que aparecen junto a una señal, siempre que la frecuencia de ésta sea fija o conocida.
Fuera de la electrónica y del procesado de señal, un ejemplo puede ser dentro del campo de las ciencias atmosféricas, donde son usados para manejar los datos dentro de un rango de 3 a 10 días.
FILTRO PASA ALTO:
El filtro paso alto más simple es un circuito RC en serie en el cual la salida es la caída de tensión en la resistencia.
Si se estudia este circuito (con componentes ideales) para frecuencias muy bajas, en continua por ejemplo, se tiene que el condensador se comporta como un circuito abierto, por lo que no dejará pasar la corriente a la resistencia, y su diferencia de tensión será cero. Para una frecuencia muy alta, idealmente infinita, el condensador se comportará como un cortocircuito, es decir, como si no estuviera, por lo que la caída de tensión de la resistencia será la misma tensión de entrada, lo que significa que dejaría pasar toda la señal. Por otra parte, el desfase entre la señal de entrada y la de salida si que varía, como puede verse en la imagen.
El producto de resistencia por condensador (R×C) es la constante de tiempo, cuyo recíproco es la frecuencia de corte, es decir, donde el módulo de la respuesta en frecuencia baja 3dB respecto a la zona pasante:
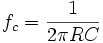
REALIZACION DEL TRABAJO PRACTICO
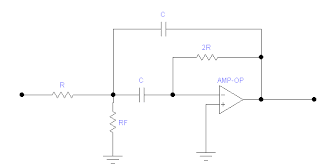
A- Armá el siguiente circuito cuidando de alimentar adecuadamente con +/- 12V sus terminales y filtrando los mismos:

B- Conéctale a la entrada Vs una señal senoidal de 200mVpp y 100Hz.
C- Medí la tensión de salida, averiguá la ganancia de tensión expresandola en veces y dB. Medí el desfasaje que sufre la señal de entrada.
Vo=2V
Ganancia en veces = 10
Ganancia en dB = 20
Desfasaje: 180º
D-Repetí elpunto anterior para no menos 20 frecuencias distintas. Aumentá el número de mediciones donde se observe un cambio significativo en algunas de ellas.
E- Elaborá una tabla donde reflejen estas mediciones y cálculos de manera ordenada y clara.

En este circuito, fc=160Hz.
F) En base a esta tabla realizá dos gráficas:
1) Una gráfica donde se muestre la variación de la ganancia expresada en dB (eje y), en función de la frecuencia (eje x). Para ellos usá un gráfico semilogarítmico. Eje y lineal, eje x expresado en décadas (también llamado decádico) comenzando con una frecuencia de 1Hz.
2) Idem anterior pero en el eje y graficá ahora el ángulo de desfasaje de la señal de salida respecto de la entrada.
El desfasaje calculado es de 139° en la fc.
G) En la primer gráfica marcar la región de paso de banda, la frecuencia de corte, y mediante mediciones logradas a partir de la tabla y/o obtenidas mismo de la gráfica calcular la pendiente de atenuación del filtro expresándolo en dB/dec. En la segunda gráfica marcá cuanto desfasa el filtro a la frecuencia de corte. Asimismo y en ese mismo gráfico marcá cuánto desfasa el filtro una década por encima y por debajo de la frecuencia de corte.
primer grafica:

segunda grafica:

tercer grafica:

cuarta grafica:

H) Aumentar dos veces el capacitor usado en el filtro y medir la nueva frecuencia de corte. Explicar cómo influye la frecuencia del capacitor en la frecuencia de corte del filtro.
fc'=87Hz
I) A manera de prueba, reemplazará el generador de señales por la salida de un reproductor de MP3. Compará la señal que te entrega este circuito. Describí esta experiencia.
Lo hicimos pero no sacamos foto, se acuerda profe que fui a comprar un mini plug 3.5mm, por favor pongame 8(ocho) ajaj.
J) Repetí los pasos 1 a 8 con el siguiente circuito:


Conclusiones finales del trabajo realizado:
Con la realización de este Trabajo Práctico, aprendimos a diseñar los filtros generalmente usados en electrónica.Aprendimos a medir sus valores y calcularlos como por ej: Resistores, Capacitores como también ancho de banda(BW),frecuencias de corte(Fc).
Aprendimos a entender las distintas gráficas de los diseños de filtro.
Disculpe por la tardanza tuvimos un problema.
No hay comentarios:
Publicar un comentario